DAG and their Topological Ordering

DAGs, directed acyclic graphs, inherently have a topological order. In fact, there are
usually multiple valid topological orderings. A topological sorting algorithm is a
procedure that produces one such valid ordering from a given DAG.

A topological ordering of a DAG is an ordered list of the DAG’s vertices where no node
\(n_j\) that can be reached by some path from node \(n_i\) appears before node \(n_i\) in
the ordering.

One way to think of it is that in a DAG, if you can get to one node \(d\) by starting at
another node \(p\), then in a sense \(p\) is kind of like one of \(d\)’s ancestor nodes. So the
rule for a topological ordering is that all ancestors must appear before their descendants
in the topological ordering.

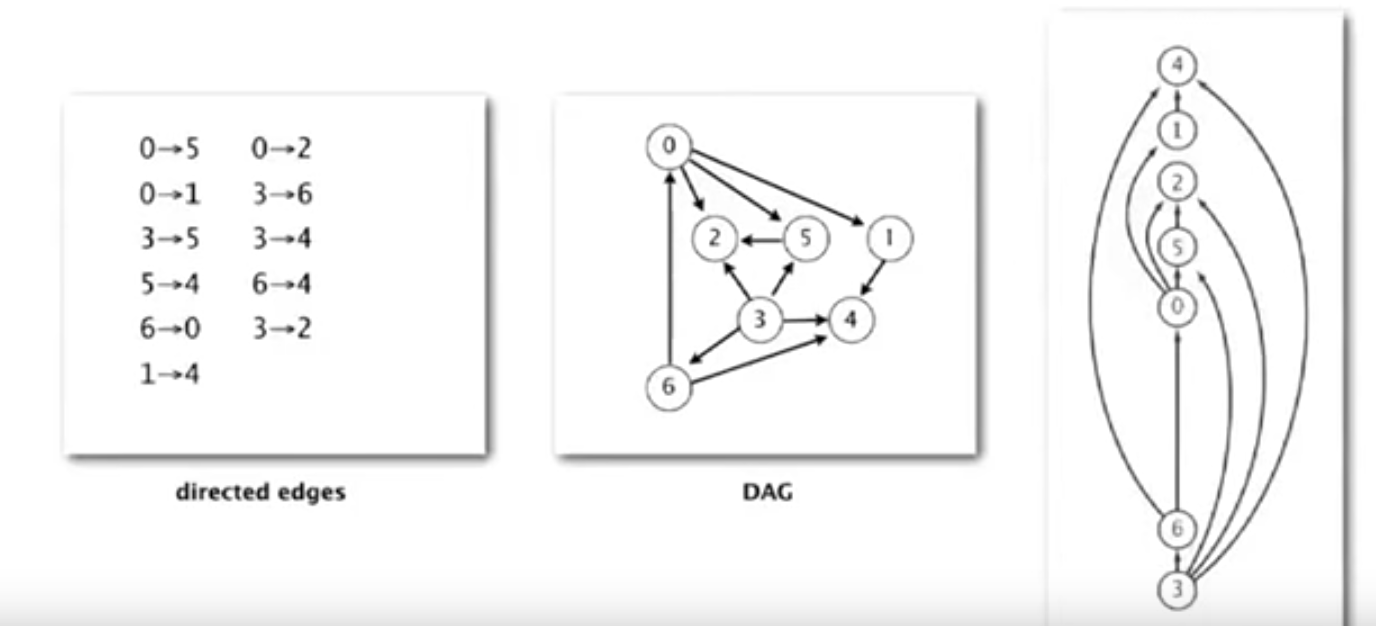
Here is a graphic to show a graph in its adjacency list form, it’s graph diagram form,
and a valid topological ordering of the graph.

Topological Sorting

The main idea in producing a topological ordering is to do a graph traversal while collecting
the search tree leaf nodes and realize that we should stick them at the end of our ordering
right off the bat. That way they’ll automatically come after their ancestors and leaf nodes
don’t have any descendants that we need to avoid putting before them in our ordering.

Well, it’s a little more complicated than that but that’s a crucial idea. In the end, a
topological sort amounts to doing a depth first search with the added condition that
every time we reach a node that has no edges leading to any other yet-unvisited node, we
push it onto a stack so that when we pop everything out of it the nodes come out in the
reverse order that they were pushed in. If we run out of places to go, we just pick any
unvisited node and keep going.

Here’s some pseudocode:

Function topsort(Graph G, Vertex V):
    Mark V as visited
    For each unvisited vertex W for which there is an edge from V to W 
        topsort(G, W)   
    Endfor
    Push V onto S
Endfunction

Initialize an empty Stack S
Algorithm Topological Sort(Graph G):
    For each unvisited vertex V in G
        topsort(G, V)
    Endfor 
    While S is not empty
        Pop a vertex V from S and print it
    Endwhile
Endalgorithm