
The goal of the QuickSelect algorithm is simple: quickly select the \(k^{th}\) smallest element in an
unsorted array of \(n\) elements. Note that the \(({n \over 2})^{th}\) smallest element is the median.
Lucky for me, a detailed explanation of how the algorithm works has already been
provided by MIT in this really good picture, so I don’t need to explain that at
all!

After we split the array into groups of five, if the number of elements in the array, \(n\), is not a
multiple of five, there will be one group at the end that does not have five elements. Let’s call
this group the “remainder group”.
So, for an array of \(n\) elements, there are at least \(ceil({n \over 5}) - 1\) non-remainder groups
of 5. This is because if \(n\) is not a multiple of 5, there will be exactly \(ceil({n \over 5}) - 1\) non-remainder
groups of 5 and one remainder group of less than 5 elements. If \(n\) is a multiple of 5, then there
will be exactly \(ceil({n \over 5}) = {n \over 5}\) groups of 5 without a remainder group left over.
Now that we have our groups of 5, let’s sort each of them separately. Since each of these groups contains
exactly 5 elements, a constant number of elements, running a sorting algorithm on each will take
constant time \(O(1)\). So, if we are doing an operation that’s \(O(1)\) for \(n \over 5\) groups, then
sorting all of those groups will take \(O(n)\). Once all the 5-element subgroups are sorted, let’s
make a set of all their medians.
Now we’re going find the median of medians by calling QuickSelect recursively on our set of medians.
Since there were \(n \over 5\) groups of 5 elements, there are also \(n \over 5\) medians from which to find the median of medians. Therefore using QuickSelect recursively on our set of medians will take \(T({n \over 5})\). Let’s
remember that for our recurrence relation much later and for now just assume we have the median of medians.
With our median of medians that we just got, we’re going to partition the array just like we did in
QuickSort, using the median of medians as the pivot: we’re going to put all elements less than the
pivot to its left and all elements greater than it to its right. If you don’t remember how that’s done
take a look at the notes on QuickSort. At this point we’ve got the array partitioned as shown in
the first diagram, so all that remains is the recurive call. But to figure out the Big-O of the recursive
call, we have to figure out the size of the sub-array we’re going to call QuickSelect on recursively.
Remember that we are using QuickSelect to get us the \(k^{th}\) smallest element. So, if after
partitioning using the median of medians, the position \(p\) of our pivot is greater than k, we clearly
have to call Quicksort on the subarray that’s less than the pivot (realize that the pivot is both at
position \(p\) and is the \(p^{th}\) smallest element since we partitioned around it). Converserly,
if, after partitioning, \(p\) is less than k, we have to call Quicksort on the subarray that’s greater
than the pivot – but now we’re looking for the \({(p-k)}^{th}\) element in that subarray since all the
elements in the subarray are greater than the \(p^{th}\) smallest element in our original array and we
were looking for the \(k^{th}\) smallest element in our original array.
So, now that we understand something about how we’ll call QuickSelect recursively on one of the two
subarrays, how do we put an upper bound on their size that’s useful for a recurrence relation so
that we can calculate QuickSelect’s Big-O? Realize that putting an upper bound on the size of these
subarrays is equivalent to putting an upper bound on the number of elements that are greater than or less
than the median of medians. Let’s start with another great picture from MIT to get us all using the same
visualization:
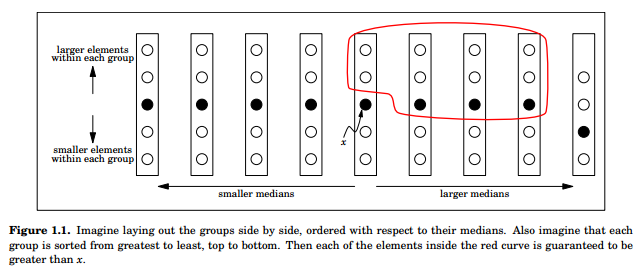
Recall that the total number of 5 element groups, including the remainder group, is \(ceil({n \over 5})\). Notice that
half of those groups can have medians that are greater than the median of medians. Well, it’s
not quite half. If there are an odd number of groups then it would actually be the rounded-down
version of half so let’s say that there are at least \(floor({1 \over 2} ceil({n \over 5}))\) groups of 5 elements
whose median is greater than the median of medians. Well, it’s not quite that number either, since
we shouldn’t count the group that actually contains the median of medians. So there are
\(floor({1 \over 2} ceil({n \over 5})) - 1\) groups with medians larger than the median of medians.
So, what then is the minumum number of elements (not groups) that are greater than the median of
medians? Well for each group whose median is greater than the median of medians, there are at least
3 elements that are greater than the median of medians. So, you’d figure that it would be 3 times
the expression we got at the end of the last paragraph. The only problem is that the expression
included the remainder group, which may not even have 3 elements, let alone 3 greater the median
of medians. So the answer is actually 3 times one less than that expression, or written in math:
\(3(floor({1 \over 2} ceil({n \over 5})) - 2)\). Oh! We almost forgot the two elements in the same
group as the median of medians that are greater than it. So our final expression for the minimum
number of elements greater than the median of medians is \(3(floor({1 \over 2} ceil({n \over 5})) - 2) + 2\). By
algebra we can show that this is greater than \({3 \over 10} n - 6\).
Alright, we managed to put a lower bound on the number of elements that are greater than the median
of medians, and this lower bound could just as easily apply to the number of elements that are
less than the median of medians too. So really, we put a lower bound on the size of the two
subarrays that we’ll be calling Quicksort on recursively. What’s more, for any expression of \(n\)
that defines a lower bound on the size of the subarrays, \(n\) minus that expression defines an
upper bound! So we finally have our upper bound on the size of these subarrays, and it’s
\(n - {3 \over 10} n - 6\ =\ {7 \over 10} n + 6\).
Therefore, the recurrence relation of Quicksort is \(T(n) = T(ceil({n \over 5})) + T({7 \over 10}n + 6) + O(n)\).
By some sneaky involved math (proof by the Substitution Method), that recurrence relation solves
to \(T(n) = O(n)\). For more information, check out this document from which I stole all the
diagrams and reasonings.
You don’t really need all that to get a quick and dirty intuition of how QuickSelect, a recursive algorithm, runs in linear time. The whole long blurb above basically just serves as proof of two things:
But most people are willing to just accept that there’s some fancy method that’s able to get something close to the median in linear time and that the actual interesting part of QuickSelect is why that means QuickSelect as a whole runs in linear time.
So what I’m going to show here is that if we can assume that finding the median takes linear time and rearranging using the median as pivot takes linear time then it’s actually pretty clear that QuickSort also takes linear time. I’ll then leave it to you to convince yourself that you can in fact get something quantifiably close enough to the median in linear time so that the intuition I’ll now provide still holds.
So given our two assumptions, why is QuickSelect \(O(n)\)? Well let’s run through it’s execution.
First we get the median in \(O(n)\) and rearrange the array into two subarrays using the median as pivot in \(O(n)\). Two operations that are \(O(n)\) is still \(O(n)\). The \(k^{th}\) smallest element will be in one of the two subarrays so we’ll repeat on one of the subarrays. Since the pivot is the perfect median the subarrays are of size exactly \(n \over 2\). Therefore the next round of median finding and rearranging is going to be \(O({n \over 2})\). If we have to recurse again then the next round will be \(O({n \over 4})\). I think you get the idea. This is a geometric whose value we know:
\[ n\ +\ \sum_{i=1}^{\infty} {1 \over {2^i}}\ =\ n\ +\ n\ =\ 2 n\ =\ O(n) \]